1 32 Decimal Equivalent: Fast Calculation Guide
Understanding the decimal equivalents of fractions is crucial in various mathematical operations, and converting 1⁄32 to its decimal form is a fundamental step in many calculations. The fraction 1⁄32 represents one part out of thirty-two equal parts of a whole. In this guide, we will explore how to quickly convert 1⁄32 into its decimal equivalent, discussing the underlying mathematical principles and providing practical tips for fast calculation.
Understanding Fractions and Decimals
Before diving into the conversion, it’s essential to grasp the basics of fractions and decimals. A fraction is a way to express a part of a whole, indicated by two numbers: the numerator (the top number) and the denominator (the bottom number). The decimal system, on the other hand, is a way of representing fractions using place value, where each place represents a power of ten.
Conversion Method
To convert 1⁄32 into a decimal, you divide the numerator by the denominator:
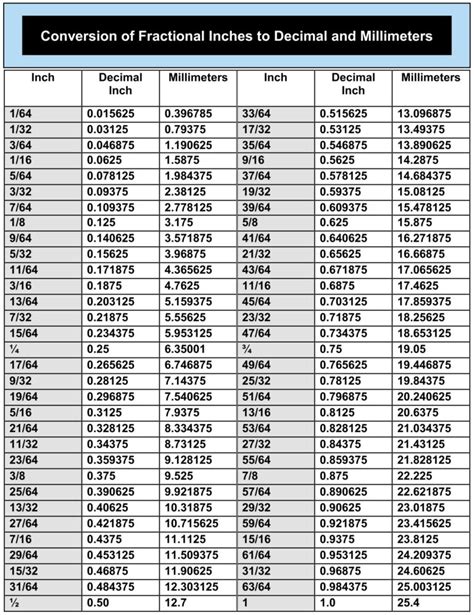
1 ÷ 32 = 0.03125
This division can be understood as sharing one unit into thirty-two equal parts, and the result, 0.03125, tells us how much of the whole one part represents in decimal form.
Fast Calculation Tips
Recognition of Patterns: Recognize that 1⁄32 is essentially 1 divided by 2^5 (since 32 = 2^5). Knowing powers of 2 can help in quick mental math. For example, 1⁄2 = 0.5, 1⁄4 = 0.25, 1⁄8 = 0.125, and so on. Each time you divide by 2, you are essentially moving the decimal point one place to the left.
Use of Known Conversions: If you already know that 1⁄8 = 0.125, you can use this to quickly find 1⁄32. Since 1⁄32 is half of 1⁄16, and 1⁄16 is half of 1⁄8, you can start with 0.125 (which is 1⁄8) and divide by 2 to get 1⁄16 (which would be 0.0625), and then divide that result by 2 again to find 1⁄32 (which is 0.03125).
Mental Math Tricks: For quick mental conversions, practice dividing numbers by powers of 10 or multiplying by powers of 10. Since decimals are essentially fractions of powers of 10, being comfortable with these operations can speed up your calculations.
Practical Applications
The conversion of 1⁄32 to its decimal equivalent, 0.03125, has practical applications in various fields, including:
- Music and Rhythm: In music, timing and rhythm can involve fractions of beats, and understanding these fractions in decimal form can aid in precision and creativity.
- Cooking and Recipes: When scaling recipes up or down, converting fractions to decimals can simplify the process, especially when dealing with ingredients that need to be measured precisely.
- Engineering and Architecture: In design and building, precise measurements are crucial. Converting fractions to decimals can ensure accuracy in plans and models, affecting the structural integrity and aesthetics of the final product.
Conclusion
Converting 1⁄32 to its decimal equivalent, 0.03125, is a straightforward process that involves dividing the numerator by the denominator. By understanding the underlying principles of fractions and decimals and applying fast calculation tips, you can efficiently perform this conversion and apply it to various practical scenarios. Practice and familiarity with these concepts will not only enhance your mathematical skills but also your ability to approach problems with confidence and precision.
Frequently Asked Questions
What is the decimal equivalent of 1/32?
+The decimal equivalent of 1/32 is 0.03125. This is found by dividing the numerator (1) by the denominator (32).
How can I quickly convert fractions to decimals?
+One way to quickly convert fractions to decimals is to recognize patterns, especially with powers of 2, and use known conversions as a starting point. For example, knowing that 1/8 = 0.125 can help you find 1/32 by dividing 0.125 by 2 to get 0.0625, and then dividing that by 2 again to find 0.03125.
What are some practical applications of converting 1/32 to a decimal?
+Converting 1/32 to a decimal has practical applications in music for timing and rhythm, in cooking for scaling recipes, and in engineering and architecture for precise measurements and designs.
By mastering the conversion of fractions to decimals, such as 1⁄32 to 0.03125, individuals can enhance their problem-solving skills, improve their understanding of mathematical concepts, and apply these skills effectively in real-world scenarios.

