Area Moment Of Inertia Circle
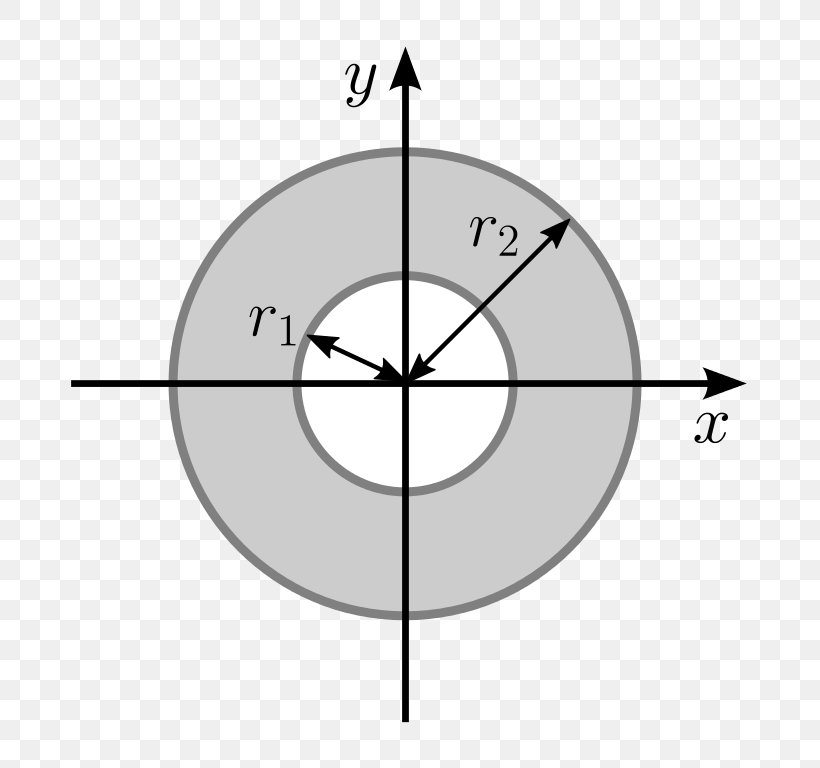
The area moment of inertia, also known as the second moment of area, is a measure of the resistance of a shape to bending and torsion. For a circle, the area moment of inertia can be calculated using the following formula:
I = πr^4 / 4
where I is the area moment of inertia, π is a mathematical constant approximately equal to 3.14159, and r is the radius of the circle.
To understand the significance of the area moment of inertia, let’s consider a simple example. Imagine a circle with a radius of 5 cm, made of a rigid material. If we were to apply a force to the circle, attempting to bend it, the circle would resist this force due to its area moment of inertia. The larger the area moment of inertia, the more resistant the circle is to bending.
The area moment of inertia of a circle is an important concept in engineering, particularly in the design of circular structures such as pipes, tubes, and cylindrical vessels. For instance, in the design of a pipeline, the area moment of inertia of the pipe’s cross-sectional area is crucial in determining its resistance to bending and torsion caused by external loads, such as soil settlement or seismic activity.
Calculation of Area Moment of Inertia for a Circle
The formula I = πr^4 / 4 can be derived by considering the circle as a collection of infinitesimally small areas, each contributing to the overall area moment of inertia. This derivation involves integrating the area of each infinitesimal element with respect to its distance from the axis of rotation, which in this case is the center of the circle.
Given the symmetry of a circle, the area moment of inertia is the same about any axis passing through its center. This is a unique property of circular shapes and is one of the reasons why circles are often used in engineering applications where symmetry and uniformity are desired.
Applications of Area Moment of Inertia in Engineering
Beam Design: The area moment of inertia is critical in the design of beams, which are structural elements that withstand loads applied laterally to the axis of the beam. The area moment of inertia of the beam’s cross-section determines its resistance to bending.
Column Design: For columns, which are subjected to axial compressive loads, the area moment of inertia is important in assessing their resistance to buckling, especially in the case of slender columns.
Shaft Design: In the design of shafts, which are subject to torsional loads, the polar moment of inertia (a related concept that applies to circular cross-sections subjected to torsion) is crucial. However, the area moment of inertia is still relevant when considering bending stresses in shafts.
Pipe Design: As mentioned earlier, the area moment of inertia is vital in the design of pipes to ensure they can withstand external pressures, internal pressures, and other environmental stresses without failing.
Key Concepts and Formulas
- Area Moment of Inertia (I): A measure of the distribution of the area of a shape around its centroidal axis. For a circle, I = πr^4 / 4.
- Radius ®: The distance from the center of the circle to its edge.
- Polar Moment of Inertia (J): For a circular cross-section, J = πr^4 / 2, which is twice the area moment of inertia about any diameter.
Real-World Examples
- Aerospace Engineering: In the design of aircraft and spacecraft, the area moment of inertia of components like wings, fuselage, and control surfaces is crucial for stability and structural integrity.
- Civil Engineering: Bridges, especially those with arch or suspension designs, rely on the area moment of inertia of their structural components to resist bending and torsional forces.
- Mechanical Engineering: The design of gears, shafts, and other machinery components often involves calculating and optimizing the area moment of inertia to ensure structural integrity under various loads.
In conclusion, the area moment of inertia of a circle is a fundamental concept in engineering that plays a critical role in the design and analysis of circular structures and components. Its calculation and application are essential in ensuring the structural integrity and performance of a wide range of engineering systems.
What is the formula for the area moment of inertia of a circle?
+The formula for the area moment of inertia of a circle is I = πr^4 / 4, where I is the area moment of inertia and r is the radius of the circle.
Why is the area moment of inertia important in engineering?
+The area moment of inertia is important because it measures a shape's resistance to bending and torsion, which is crucial in the design of structures and components to ensure they can withstand various loads without failing.
How does the area moment of inertia apply to real-world engineering problems?
+The area moment of inertia applies to the design of beams, columns, shafts, pipes, and other structural elements, helping engineers determine the resistance of these elements to bending and torsional forces.
The significance of the area moment of inertia in engineering design cannot be overstated. It is a fundamental principle used across various disciplines to ensure the structural integrity and performance of components and systems. As engineering continues to evolve, understanding and applying the concept of area moment of inertia will remain vital for the development of safe, efficient, and innovative solutions.