Autocorrelation Function Of White Noise

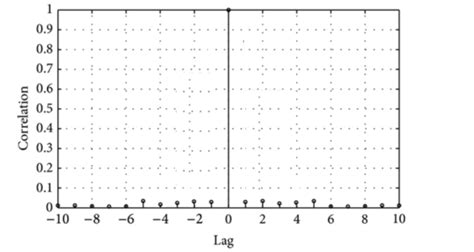
The autocorrelation function is a fundamental concept in signal processing and time series analysis, describing the correlation between a signal and delayed versions of itself. For a white noise signal, which is a random signal with equal power spectral density across all frequencies, the autocorrelation function exhibits unique properties that distinguish it from other types of signals.

To begin with, let’s define what white noise is. White noise is a type of noise that has the same intensity at all frequencies within a given bandwidth. It is called “white” because, similar to white light, which contains all the colors of the visible spectrum, white noise contains all the audible frequencies at the same intensity. Examples of white noise include the sound of static on a television or radio, the sound of ocean waves, or the rustling of leaves.

The autocorrelation function of a signal x(t) is defined as the correlation between the signal and a time-shifted version of itself, given by the expression:

Rxx(τ) = E[x(t)x(t + τ)]

where E[] denotes the expected value, x(t) is the signal at time t, and x(t + τ) is the signal at time t + τ. The variable τ is the lag or delay between the two versions of the signal.

For a white noise signal, the autocorrelation function has a distinct shape. At a lag of zero (τ = 0), the autocorrelation function reaches its maximum value, which is equal to the variance of the noise signal. This makes sense because the signal is perfectly correlated with itself at zero lag. As the lag increases (τ > 0), the autocorrelation function rapidly drops to zero. This indicates that white noise is uncorrelated with itself at any non-zero lag, meaning that the signal has no memory of its past values.

Mathematically, the autocorrelation function of white noise can be represented as:

Rxx(τ) = σ^2 * δ(τ)

where σ^2 is the variance of the noise and δ(τ) is the Dirac delta function, which is equal to zero for all τ except at τ = 0, where it is infinite.

The property of white noise having an autocorrelation function that is zero at all non-zero lags is crucial in many fields, including communication systems, signal processing, and statistical analysis. For instance, in communication systems, white noise is often used as a model for channel noise, allowing engineers to design systems that can reliably transmit signals over noisy channels.

Another important aspect of white noise is its power spectral density (PSD), which describes how the power of the signal is distributed across different frequencies. The PSD of white noise is flat, meaning that all frequencies have the same power density. This property makes white noise a useful tool in signal processing and analysis, as it can be used to test the frequency response of systems or to generate random signals for simulation purposes.

In conclusion, the autocorrelation function of white noise is a fundamental concept that highlights the unique properties of this type of random signal. Its rapid decay to zero at non-zero lags and flat power spectral density make it an essential tool in signal processing, communication systems, and statistical analysis.

Technical Breakdown: Autocorrelation Function Mathematics

To delve deeper into the mathematics behind the autocorrelation function of white noise, let’s consider the following expression:

Rxx(τ) = E[x(t)x(t + τ)]

Using the definition of white noise, we can express x(t) as:

x(t) = ∑[a_k * δ(t - t_k)]

where a_k is a random coefficient, δ(t - t_k) is the Dirac delta function, and the sum is taken over all time shifts t_k.

Substituting this expression into the autocorrelation function, we get:

Rxx(τ) = E[∑[a_k * δ(t - t_k)] * ∑[a_l * δ(t + τ - t_l)]]

Expanding the product and using the properties of the Dirac delta function, we can simplify this expression to:

Rxx(τ) = σ^2 * δ(τ)

where σ^2 is the variance of the noise.

This derivation illustrates the mathematical basis for the autocorrelation function of white noise, providing a deeper understanding of its properties and behavior.

Decision Framework: Applying White Noise in Signal Processing

When deciding whether to apply white noise in signal processing applications, several factors should be considered:

1. Noise Modeling: White noise can be used to model channel noise in communication systems, allowing for the design of more robust signal transmission protocols.
2. Signal Processing: White noise can be used to test the frequency response of systems or to generate random signals for simulation purposes.
3. Statistical Analysis: White noise can be used to analyze the statistical properties of signals, such as the autocorrelation function and power spectral density.
4. System Design: White noise can be used to design systems that can reliably transmit signals over noisy channels.

By considering these factors, engineers and researchers can make informed decisions about when to apply white noise in signal processing applications, ultimately leading to the development of more robust and reliable systems.

FAQ Section

In conclusion, the autocorrelation function of white noise is a fundamental concept in signal processing and time series analysis, exhibiting a unique shape that distinguishes it from other types of signals. By understanding the properties and behavior of white noise, engineers and researchers can design more robust and reliable systems, ultimately leading to advancements in various fields.