Convert To Polar Coordinates Calculator

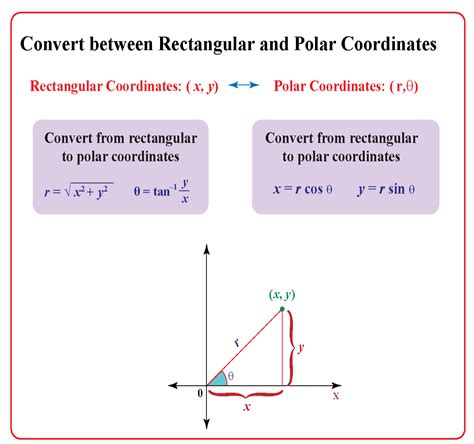
Converting between Cartesian (rectangular) coordinates and polar coordinates is a fundamental concept in mathematics, particularly in geometry, trigonometry, and calculus. The conversion process involves changing the representation of a point in a two-dimensional plane from (x, y) coordinates to (r, \theta), where r is the radius or distance from the origin to the point, and \theta is the angle from the positive x-axis to the line segment that connects the origin to the point.

Introduction to Polar Coordinates

Polar coordinates offer a convenient way to describe points in a plane when the distance from a reference point (origin) and the direction from the reference point are known. This coordinate system is especially useful in physics, engineering, and other fields where rotational motion, circular paths, or directional quantities are involved.

Conversion Formulas

To convert from Cartesian (x, y) to polar (r, \theta) coordinates, you use the following formulas:

1. Radius ®: Calculated using the formula r = \sqrt{x^2 + y^2}. This formula is derived from the Pythagorean theorem, as it represents the hypotenuse of a right triangle formed by the x and y coordinates.

2. Angle (\theta): Calculated using the formula \theta = \arctan\left(\frac{y}{x}\right). However, the quadrant of (x, y) must be considered to ensure \theta is in the correct range. The arctan function returns values in the range -\frac{\pi}{2} to \frac{\pi}{2}, but \theta should be adjusted based on the sign of x and y to fall within the range [0, 2\pi).

Adjusting \theta Based on Quadrant

• If x > 0 and y \geq 0, \theta = \arctan\left(\frac{y}{x}\right).
• If x < 0 and y \geq 0, \theta = \pi + \arctan\left(\frac{y}{x}\right).
• If x < 0 and y < 0, \theta = \pi + \arctan\left(\frac{y}{x}\right).
• If x > 0 and y < 0, \theta = 2\pi + \arctan\left(\frac{y}{x}\right).

Calculator Implementation

A converter from Cartesian to polar coordinates can be implemented in various programming languages or as an online tool. Here’s a simple example of how it might look in Python:

import math

def cartesian_to_polar(x, y):
    r = math.sqrt(x2 + y2)
    theta = math.atan2(y, x)  # math.atan2 handles quadrant adjustment
    
    # Optional: Convert theta from radians to degrees
    theta_degrees = math.degrees(theta)
    
    return r, theta, theta_degrees

# Example usage
x = 3
y = 4
r, theta, theta_degrees = cartesian_to_polar(x, y)

print(f"Radius (r): {r}")
print(f"Angle (θ) in radians: {theta}")
print(f"Angle (θ) in degrees: {theta_degrees}")

Practical Applications

The conversion to polar coordinates has numerous practical applications, including:

• Navigation and Direction: In aviation, nautical, and automotive navigation, where directions and distances are crucial.
• Robotics and Computer Vision: For robots to understand their environment and move accordingly, polar coordinates can be more intuitive than Cartesian coordinates.
• Medical Imaging: In medical imaging technologies like MRI and CT scans, polar coordinates can help in analyzing and representing anatomical structures.

Conclusion

Converting Cartesian coordinates to polar coordinates involves straightforward mathematical formulas but requires attention to the quadrant in which the point lies to correctly determine the angle \theta. Understanding and applying these conversions can facilitate problem-solving in various scientific and engineering disciplines.