Math Geometry: Learn Key Definitions

Understanding the fundamentals of math geometry is crucial for grasping more complex concepts in mathematics, engineering, architecture, and other fields. Geometry, which literally means “earth measurement” in Greek, involves the study of shapes, sizes, and positions of objects. It encompasses various branches, including point geometry, line geometry, and solid geometry, each focusing on different aspects of geometric objects.

Points, Lines, and Planes: The Building Blocks

In geometry, the most basic elements are points, lines, and planes.

• Points are considered to have no size, only location. They are often represented by coordinates (x, y) in a two-dimensional plane or (x, y, z) in three-dimensional space.
• Lines are sets of points extending infinitely in two directions. They can be straight or curved. A line can be defined by two distinct points.
• Planes are flat surfaces that extend infinitely in all directions. A plane can be defined by three points that are not on the same line.

Angles and Measurements

Angles are formed by two rays (or lines) sharing a common endpoint, known as the vertex. The size of an angle is measured in degrees, with a full circle being 360 degrees. Key angle measurements include:

• Acute Angle: Less than 90 degrees.
• Right Angle: Exactly 90 degrees.
• Obtuse Angle: Greater than 90 degrees but less than 180 degrees.
• Straight Angle: Exactly 180 degrees.

Understanding angles is crucial for calculating distances, heights, and other geometric properties.

Geometric Shapes

Geometric shapes are the core of geometry and include:

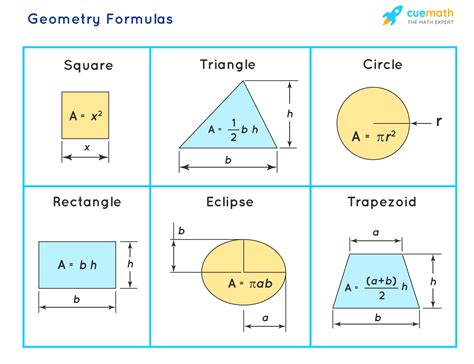
• Triangles: Three-sided shapes with three vertices and three angles. The sum of the angles in a triangle is always 180 degrees.
• Quadrilaterals: Four-sided shapes. Special types include rectangles (opposite sides are equal and all angles are right angles) and squares (a special rectangle where all sides are equal).
• Polygons: Many-sided shapes. The internal angles of any polygon can be calculated using the formula (n-2)*180 degrees, where n is the number of sides.
• Circles: Continuous curved shapes where every point on the circle is equidistant from a central point called the center. The distance from the center to any point on the circle is the radius.

Properties and Theorems

Several properties and theorems are essential in geometry, including:

• Congruence: Two figures are congruent if one can be transformed into the other through rotation, reflection, or translation without changing their size or shape.
• Similarity: Two figures are similar if one can be transformed into the other through scaling (enlarging or reducing), rotation, reflection, or translation.
• Pythagorean Theorem: In a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.

Applications of Geometry

Geometry is not just about abstract concepts; it has numerous practical applications in:

• Architecture: For designing buildings and other structures.
• Engineering: In the design of bridges, roads, and electronic circuits.
• Computer Graphics: For creating 3D models and animations.
• GPS Navigation: Uses geometric principles to calculate distances and positions.

Conclusion

Geometry is a vast and complex field that underpins many areas of science, technology, engineering, and mathematics (STEM). Understanding its key definitions and concepts is essential for solving problems, both practically and theoretically. As technology advances, the role of geometry in innovation and problem-solving continues to grow, making it a fundamental body of knowledge for anyone involved in these fields.

Understanding geometry requires a solid grasp of its definitions, concepts, and how these are applied in different contexts. As with any complex subject, practice and exploration are key to mastering geometry and unlocking its vast potential in solving problems and driving innovation.