Moment Of Intertia Rod
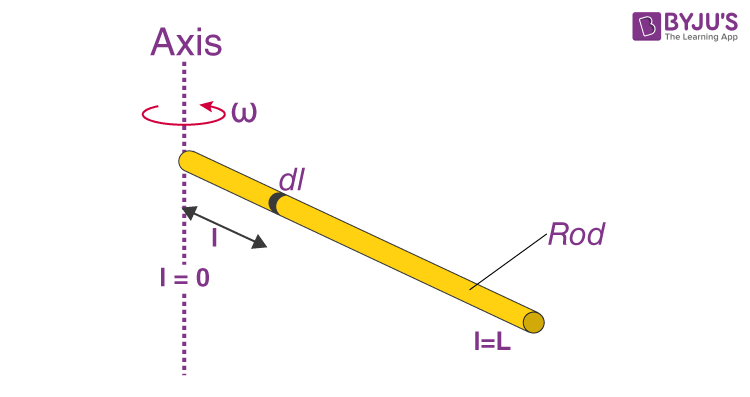
The moment of inertia of a rod is a fundamental concept in physics, particularly in the fields of mechanics and engineering. It is a measure of an object’s resistance to changes in its rotation, and it plays a crucial role in understanding various phenomena, such as the behavior of rotating systems, the stability of structures, and the performance of mechanical devices.
To understand the moment of inertia of a rod, let’s first define what a rod is. A rod is a long, slender object with a fixed cross-sectional area, typically circular or rectangular in shape. When a rod is rotated about an axis, it experiences a torque, which is a force that causes it to rotate. The moment of inertia of the rod is a measure of its resistance to this rotational force.
The moment of inertia of a rod depends on its mass, length, and cross-sectional area. For a rod of length L and mass M, the moment of inertia (I) about an axis perpendicular to the rod and passing through its center of mass is given by the following equation:
I = (1⁄12) * M * L^2
This equation shows that the moment of inertia of a rod is directly proportional to its mass and the square of its length. This means that a longer or more massive rod will have a greater moment of inertia, making it more resistant to changes in its rotation.
Now, let’s consider a few examples to illustrate the concept of moment of inertia of a rod. Imagine a gymnast performing a routine on a balance beam. The gymnast’s body can be approximated as a rod, and their moment of inertia will depend on their mass, height, and the distribution of their body mass. When the gymnast rotates their body, they experience a torque that causes them to rotate, and their moment of inertia determines their resistance to this rotational force.
Another example is a helicopter rotor blade, which can be modeled as a rod. The moment of inertia of the rotor blade is critical in determining the stability and performance of the helicopter. A higher moment of inertia means that the rotor blade will be more resistant to changes in its rotation, which can affect the helicopter’s ability to maneuver and respond to control inputs.
In addition to these examples, the moment of inertia of a rod has numerous applications in fields such as mechanical engineering, aerospace engineering, and materials science. For instance, engineers use the moment of inertia to design and optimize mechanical systems, such as gearboxes, shafts, and bearings, to ensure efficient and reliable operation.
To further illustrate the concept of moment of inertia, let’s consider a few key points:
- Moment of inertia about different axes: The moment of inertia of a rod can be calculated about different axes, depending on the orientation of the rod and the axis of rotation. For example, the moment of inertia about an axis perpendicular to the rod and passing through its center of mass is different from the moment of inertia about an axis parallel to the rod.
- Moment of inertia of composite systems: When multiple rods are connected to form a composite system, the moment of inertia of the system can be calculated by summing the moments of inertia of each individual rod.
- Effect of density on moment of inertia: The density of the material from which the rod is made affects its moment of inertia. A rod made from a denser material will have a higher moment of inertia than a rod made from a less dense material, assuming the same length and cross-sectional area.
In conclusion, the moment of inertia of a rod is a critical concept in understanding the behavior of rotating systems and the performance of mechanical devices. By understanding the factors that affect the moment of inertia of a rod, engineers and physicists can design and optimize systems to achieve specific goals, such as improving stability, efficiency, or responsiveness.
Comparative Analysis of Moment of Inertia of Different Shapes
To further illustrate the concept of moment of inertia, let’s compare the moment of inertia of different shapes, such as rods, disks, and spheres. Each shape has a unique moment of inertia, which depends on its mass, size, and distribution of mass.
| Shape | Moment of Inertia |
|---|---|
| Rod | (1⁄12) * M * L^2 |
| Disk | (1⁄2) * M * R^2 |
| Sphere | (2⁄5) * M * R^2 |
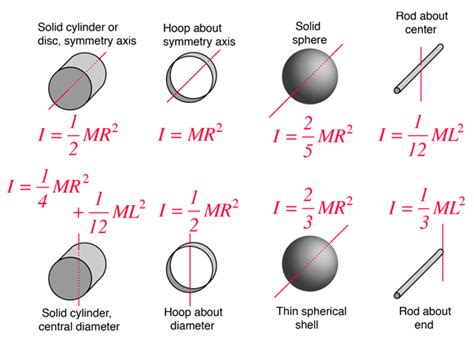
As shown in the table, the moment of inertia of each shape depends on its mass (M), size (L or R), and distribution of mass. The rod has a moment of inertia that is directly proportional to its mass and the square of its length, while the disk and sphere have moments of inertia that are proportional to their mass and the square of their radius.
Decision Framework for Selecting the Optimal Shape
When designing a mechanical system or device, engineers must consider the moment of inertia of different shapes to select the optimal shape for the application. Here’s a decision framework to help select the optimal shape:
- Define the application requirements: Identify the specific requirements of the application, such as the desired rotational speed, torque, and stability.
- Calculate the moment of inertia: Calculate the moment of inertia of different shapes, such as rods, disks, and spheres, using the formulas provided earlier.
- Compare the moments of inertia: Compare the moments of inertia of different shapes to determine which shape has the desired moment of inertia for the application.
- Consider additional factors: Consider additional factors, such as the material properties, manufacturing constraints, and cost, to select the optimal shape for the application.
By following this decision framework, engineers can select the optimal shape for their application, taking into account the moment of inertia and other critical factors.
What is the moment of inertia of a rod?
+The moment of inertia of a rod is a measure of its resistance to changes in its rotation, and it depends on its mass, length, and cross-sectional area. The moment of inertia of a rod is given by the equation I = (1⁄12) * M * L^2.
How does the moment of inertia of a rod affect its rotation?
+The moment of inertia of a rod affects its rotation by determining its resistance to changes in its rotational speed. A higher moment of inertia means that the rod will be more resistant to changes in its rotation, while a lower moment of inertia means that it will be less resistant.
What are some applications of the moment of inertia of a rod?
+The moment of inertia of a rod has numerous applications in fields such as mechanical engineering, aerospace engineering, and materials science. It is used to design and optimize mechanical systems, such as gearboxes, shafts, and bearings, to ensure efficient and reliable operation.



