Polar Rectangular Calculator
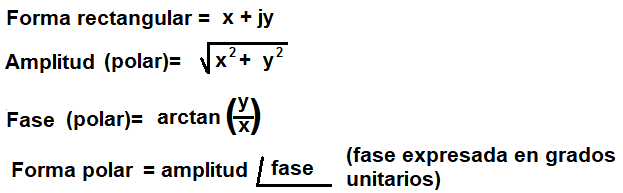
The realm of coordinate systems is a fundamental aspect of mathematics, particularly in the fields of geometry, trigonometry, and engineering. Within this vast domain, the polar and rectangular (or Cartesian) coordinate systems are two of the most commonly used frameworks for representing points in a plane. Each system has its unique advantages and applications, and the ability to convert between them is a crucial skill for anyone working in these fields. This article delves into the nuances of a polar rectangular calculator, a tool designed to facilitate conversions between these two essential coordinate systems.
Introduction to Coordinate Systems
Before diving into the specifics of the calculator, it’s essential to understand the basics of both polar and rectangular coordinate systems.
Rectangular (Cartesian) Coordinate System: This is the most commonly used coordinate system, where each point on a plane is determined by an ordered pair of numbers (x, y). The x-axis and y-axis intersect at a point known as the origin. The x-coordinate represents the horizontal distance from the origin, and the y-coordinate represents the vertical distance.
Polar Coordinate System: In contrast, the polar coordinate system represents points using a distance from a reference point (the origin) and the angle formed with the positive x-axis (measured in radians and denoted by θ). Thus, a point in the polar system is represented as (r, θ), where r is the radius or distance from the origin to the point, and θ is the angle.
The Need for Conversion
The need to convert between polar and rectangular coordinates arises from the fact that certain mathematical operations and geometric representations are more naturally suited to one system over the other. For instance, circular motions and relationships involving angles are often more straightforward in polar coordinates, whereas rectangular coordinates are better suited for representing linear relationships and structures aligned with the axes.
Polar Rectangular Calculator: Functionality
A polar rectangular calculator is a mathematical tool that allows users to convert between polar and rectangular coordinates easily. The basic functionality involves inputting either the polar coordinates (r, θ) or the rectangular coordinates (x, y) and then computing the equivalent coordinates in the other system.
From Polar to Rectangular: Given (r, θ), the conversion to rectangular coordinates (x, y) can be achieved using the following formulas:
- (x = r \cos(\theta))
- (y = r \sin(\theta))
From Rectangular to Polar: Conversely, given (x, y), the conversion to polar coordinates (r, θ) involves:
- (r = \sqrt{x^2 + y^2})
- (\theta = \tan^{-1}\left(\frac{y}{x}\right))
Note that the calculation of θ must consider the quadrant in which (x, y) lies to ensure the correct angle.
Implementing the Calculator
Implementing a polar rectangular calculator can be straightforward using programming languages or even spreadsheet software. The core of the implementation involves coding the conversion formulas and handling the input/output operations. For developers, libraries that support trigonometric functions (such as cosine, sine, and arctangent) are essential.
Example Usage
To illustrate the usage, let’s consider converting the polar coordinates (5, π/4) to rectangular coordinates:
- Input: (r = 5), (\theta = \frac{\pi}{4})
- Conversion:
- (x = 5 \cos\left(\frac{\pi}{4}\right) = 5 \times \frac{\sqrt{2}}{2} = \frac{5\sqrt{2}}{2})
- (y = 5 \sin\left(\frac{\pi}{4}\right) = 5 \times \frac{\sqrt{2}}{2} = \frac{5\sqrt{2}}{2})
Thus, the rectangular coordinates are (\left(\frac{5\sqrt{2}}{2}, \frac{5\sqrt{2}}{2}\right)).
Advanced Considerations
While the basic functionality of a polar rectangular calculator is straightforward, there are several advanced considerations that can enhance its utility:
- Handling Quadrants: Automatic detection of the quadrant for (\theta) when converting from rectangular to polar coordinates to ensure the correct angle.
- Input Validation: Checking for valid input ranges, especially for (\theta), which should be within (0) to (2\pi) for a full circle representation.
- Precision Control: Allowing users to set the precision of the output to accommodate different requirements.
Conclusion
A polar rectangular calculator is an indispensable tool for anyone working with coordinate systems, providing a quick and reliable means to convert between polar and rectangular coordinates. Whether used in educational settings to illustrate mathematical concepts or in professional environments for design and calculation purposes, its utility is undeniable. By understanding the principles behind such a calculator and its applications, users can harness the full potential of coordinate systems in mathematics and beyond.
FAQ Section
What are the primary applications of a polar rectangular calculator?
+The primary applications include educational purposes to teach coordinate systems, professional use in fields like engineering and physics for calculations involving circular motions and geometric shapes, and in programming for game development and graphical representations.
How do I handle the conversion when the angle θ is not in radians?
+If θ is given in degrees, you need to convert it to radians first using the formula (radians = degrees \times \frac{\pi}{180}) before applying the conversion formulas.
What considerations should I keep in mind when implementing a polar rectangular calculator?
+Key considerations include input validation to ensure that values are within expected ranges, handling of quadrants to correctly calculate the angle θ, and precision control to meet specific application requirements.
